Simulating Wavefunctions within Various Potential Wells using Schrödinger's Wave Equation

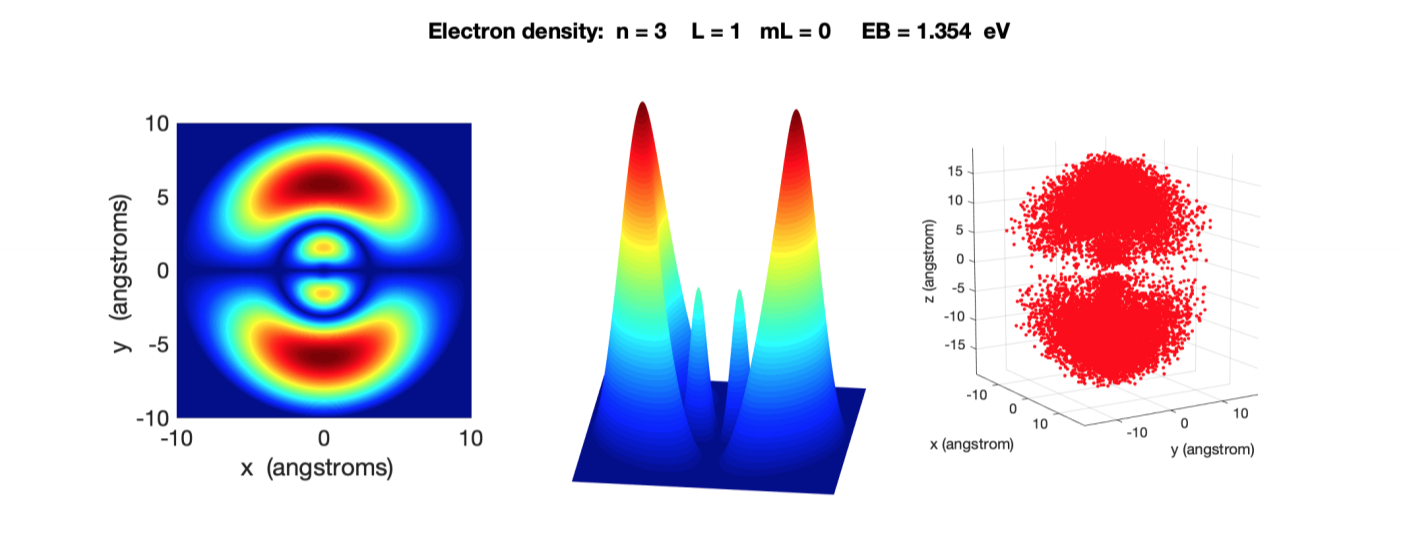
In the quantum scale the particles act according to a wave-like behavior. Therefore, a given quantum particle can be represented as a wavefunction which can be related to the space and time coordinates using the Schrödinger equation.

Studying about the solutions that Schrödinger equation provides under different potential conditions (one dimensional, two dimensional and three dimensional) and boundary conditions is a powerful way of gaining a valuable insight into quantum mechanics. However, analytically solving the Schrödinger equation is a tedious task and it is only possible for a few given potential functions. In this work, we will consider a few numerical methods such as Finite Difference Method, Numerov’s Matrix Method and Finite Elements Method. These methods are able to provide solutions for the time independent Schrödinger equation under various potential conditions for one dimensional, two dimensional and three dimensional scenarios. keywords — Time Independent Schrödinger Equation, Finite Difference Method,Numerov’s Matrix Method, Finite Elements Method.

Grade : 4.2/4.2

Supervisor(s) : Dr. Mewan Gunawardena

Report : [Report]

Code : [Code]